Формула магнитной индукции бесконечного проводника с током. Закон Био-Савара-Лапласа и его применение к расчету магнитного поля прямого и кругового токов

Пусть вдоль осиOZ расположен бесконечно длинный проводник, по которому течёт ток с силой . А сила тока это что такое?

,

- заряд, который пересекает поверхностьS за время

. Система обладает осевой симметрией. Если мы введём цилиндрические координатыr ,  , z , то цилиндрическая симметрия означает, что

и, кроме того,

, при смещении вдоль осиOZ , мы видим то же самое. Таков источник. Магнитное поле должно быть таким, чтобы удовлетворялись эти условия

и

. Это означает вот что: силовые линии магнитного поля – окружности, лежащие в плоскости ортогональной проводнику. Это немедленно позволяет найти магнитное поле.

Пусть у нас это проводник.

Вот ортогональная плоскость,

вот окружность радиуса r ,

я возьму тут касательный вектор, вектор, направленный вдоль  , касательный вектор к окружности.

Тогда,

,

где

.

В качестве замкнутого контура выбираем окружность радиуса r = const . Пишем тогда , сумма длин по всей окружности (а интеграл это ни что иное, как сумма) – это длина окружности., где – сила тока в проводнике. Справа стоит заряд, который пересекает поверхность за единицу времени. Отсюда мораль:

. Значит, прямой проводник создаёт магнитное поле с силовыми линиями в виде окружностей, охватывающих проводник, и эта величинаВ убывает как при удалении от проводника, ну, и стремится к бесконечности, если мы приближаемся к проводнику, когда контур уходит внутрь проводника.

Этот результат только для случая, когда контур охватывает ток. Понятно, что бесконечный проводник нереализуем. Длина проводника, – наблюдаемая величина, и никакие наблюдаемые величины не могут принимать бесконечных значений, не такой линейки, которая позволила бы измерить бесконечную длину. Это нереализуемая вещь, тогда какой толк в этой формуле? Толк простой. Для любого проводника, будет справедливо следующее: достаточно близко к проводнику силовые линии магнитного поля – вот такие замкнутые окружности, охватывающие проводник, и на расстоянии

(R – радиус кривизны проводника), будет справедлива эта формула.

Магнитное поле, создаваемое произвольным проводником с током.

Закон Био-Савара.

Пусть мы имеем произвольный проводник с током, и нас интересует магнитное поле, создаваемое куском этого проводника в данной точке. Как, кстати, в электростатике находили мы электрическое поле, создаваемое каким-то распределением заряда? Распределение разбивали на малые элементы и вычисляли в каждой точке поле от каждого элемента (по закону Кулона) и суммировали. Такая же программа и здесь. Структура магнитного поля сложнее, чем электростатическое, кстати, оно не потенциально, замкнутое магнитное поле нельзя представить как градиент скалярной функции, у него другая структура, но идея та же самая. Разбиваем проводник на малые элементы. Вот я взял маленький элемент

, положение этого элемента определяется радиус-вектором, а точка наблюдения задаётся радиус-вектором. Утверждается, что этот элемент проводника создаст в этой точке индукциюпо такому рецепту:

. Откуда берётся этот рецепт? Его нашли в своё время экспериментально, трудно мне, кстати, представить, как это можно было экспериментально найти такую достаточно сложную формулу с векторным произведением. На самом деле это следствие четвёртого уравнения Максвелла

. Тогда поле, создаваемое всем проводником:

, или, мы можем написать теперь интеграл:

. Понятно, что вычислять такой интеграл для произвольного проводника занятие не очень приятное, но в виде суммы это нормальная задача для компьютера.

Пример. Магнитное поле кругового витка с током.

Пусть в плоскостиYZ располагается проволочный виток радиуса R, по которому течёт ток силы . Нас интересует магнитное поле, которое создаёт ток. Силовые линии вблизи витка такие:

Общая картина силовых линий тоже просматривается (рис.7.10 ).

По идее, нас интересовало бы поле

, но в элементарных функциях указать поле этого витка нельзя. Найти можно только на оси симметрии. Мы ищем поле в точках (х ,0,0).

Направление вектора определяется векторным произведением

. Векторимеет две составляющие:

и. Когда мы начнём суммировать эти вектора, то все перпендикулярные составляющие в сумме дадут ноль.

. А теперь пишем:

,

=, а

.

, и, наконец 1) ,

.

Мы добыли такой результат:

А теперь, в качестве проверки, поле в центре витка равна:

.

Поле длинного соленоида.

Соленоидом называется катушка, на которую намотан проводник.

Магнитное поле от витков складывается, и не трудно догадаться, что структура силовых линий поля такая: они внутри идут густо, а дальше разреженно. То есть для длинного соленоида снаружи будем считать=0, а внутри соленоида=const . Внутри длинного соленоида, ну, в окрестности. Скажем, его середины, магнитное поле практически однородно, а вне соленоида это поле мало. Тогда мы можем найти это магнитное поле внутри следующим образом: вот я беру такой контур (рис.7.13 ), а теперь пишем:

1)





.

- это полный заряд. Эту поверхность протыкают витки

(полный заряд)=

(число витков, протыкающих эту поверхность).

Мы получим такое равенство из нашего закона:

, или

.

Поле на большом расстоянии от ограниченного распределения тока.

Магнитный момент

Имеется в виду, что в ограниченной области пространства текут токи, тогда есть простой рецепт для нахождения магнитного поля, которое создаёт это ограниченное распределение. Ну, кстати, под это понятие ограниченное пространство подпадает любой источник, поэтому тут никакого сужения нет.

Если характерный размер системы , то

. Напомню, что мы решали аналогичную проблему для электрического поля, создаваемого ограниченным распределением заряда, и там появилось понятие дипольного момента, и моментов более высокого порядка. Решать эту задачу я здесь не буду.

По аналогии (как делалось в электростатике) можно показать, что магнитное поле от ограниченного распределения на больших расстояниях подобно электрическому полю диполя. То есть структура этого поля такая:

Распределение характеризуется магнитным моментом .Магнитный момент

, где– плотность тока или, если учесть, что мы имеем дело с движущимися заряженными частицами, то вот эту формулу для сплошно среды мы можем выразить через заряды частиц таким образом:

. Что эта сумма выражает? Повторяю, распределение тока создаётся тем, что движутся эти заряженные частицы. Радиус-векторi -ой частицы векторно умножается на скорость i -ой частицы и всё это умножается на заряд этой i -ой частицы.

Такая конструкция, кстати, у нас в механике была. Если вместо заряда без множителя написать массу частицы, то, что это будет изображать? Момент импульса системы.

Если мы имеем частицы одного сорта (

, например, электроны), то тогда мы можем написать



. Значит, если ток создаётся частицами одного сорта, то магнитный момент связан просто с моментом импульса этой системы частиц.

Магнитное поле , создаваемое этим магнитным моментом равно:

(8.1 )

Магнитный момент витка с током

Пусть у нас имеется виток и по нему течёт ток силы. Вектор отличен от нуля в пределах витка. Возьмём элемент этого витка,

, гдеS – поперечное сечение витка, а – единичный касательный вектор. Тогда магнитный момент определён так:

. А что такое

? Это вектор, направленный вдоль вектора нормали к плоскости витка. А векторное произведение двух векторов – это удвоенная площадь треугольника, построенного на этих векторах. ЕслиdS – площадь треугольника, построенного на векторах и, то

. Тогда мы пишем магнитный момент равняется. Значит,

(магнитный момент витка с током)=(сила тока)(площадь витка)(нормаль к витку) 1) .

А теперь мы формулу (8.1 ) применим для витка с током и сопоставим с тем, что мы добыли в прошлый раз, просто для проверки формулы, поскольку формулу эту я слепил по аналогии.

Пусть мы имеем в начале координат виток произвольной формы, по которому течёт ток силы , тогда поле в точке на расстоянии х равно: (

). Для круглого витка

,

. На прошлой лекции мы находили магнитное поле круглого витка с током, при

эти формулы совпадают.

На больших расстояниях от любого распределения тока магнитное поле находится по формуле (8.1 ), а всё это распределение характеризуется одним вектором, который называется магнитный момент. Кстати, простейший источник магнитного поля это магнитный момент. Для электрического поля простейший источник это монополь, для электрического поля следующий по сложности это электрический диполь, а для магнитного поля всё начинается с этого диполя или магнитного момента. Это, ещё раз обращаю внимание, постольку, поскольку нет этих самых монополей. Был бы монополь, тогда было бы всё также как в электрическом поле. А так у нас простейший источник магнитного поля это магнитный момент, аналог электрического диполя. Наглядный пример магнитного момента – постоянный магнит. Постоянный магнит обладает магнитным моментом, и на большом расстоянии его поле имеет такую структуру:

Сила, действующая на проводник с током в магнитном поле

Мы видели, что на заряженную частицу действует сила, равная

. Ток в проводнике есть результат движения заряженных частиц тела, то есть равномерно размазанного заряда в пространстве нет, заряд локализован в каждой частице. Плотность тока

. Наi -ую частицу действует сила

.

Выберем элемент объёма

и просуммируем силы, действующие на все частицы этого элемента объёма

. Сила, действующая на все частицы в данном элементе объёма, определяется как плотность тока на магнитное поле и на величину элемента объёма. А теперь перепишем её в дифференциальном виде:

, отсюда

– этоплотность силы , сила, действующая на единицу объёма. Тогда мы получим общую формулу для силы:

.

Обычно ток течёт по линейным проводникам, редко мы сталкиваемся с случаями, когда ток размазан как-то по объёму. Хотя, между прочим, Земля имеет магнитное поле, а от чего это поле? Источник поля это магнитный момент, это означает, что Земля обладает магнитным моментом. А это означает, что тот рецепт для магнитного момента показывает, что должны быть какие-то токи внутри Земли, они по необходимости должны быть замкнутыми, потому что не может быть стационарного разомкнутого поля. Откуда эти токи, что их поддерживает? Я не специалист в земном магнетизме. Какое-то время назад определённой модели этих токов ещё не было. Они могли быть там когда-то индуцированы и ещё не успели там затухнуть. На самом деле, ток можно возбудить в проводнике, и потом он быстро сам кончается за счёт поглощения энергии, выделения тепла и прочего. Но, когда мы имеем дело с такими объёмами как Земля, то там время затухания этих токов, однажды каким-то механизмом возбуждённых, это время затухания может быть очень длительным и длиться геологические эпохи. Может быть, так оно и есть. Ну, скажем, мелкий объект типа Луны имеет очень слабое магнитное поле, это означает, что оно затухло там уже, скажем, магнитное поле Марса тоже значительно слабее поля Земли, потому что и марс меньше Земли. Это я к чему? Конечно, есть случаи, когда токи текут в объёмах, но то, что мы здесь на Земле имеем это обычно линейные проводники, поэтому эту формулу сейчас трансформируем применительно к линейному проводнику.

Пусть имеется линейный проводник, ток течёт с силой. Выберем элемент проводника , объём этого элементаdV ,

,

. Сила, действующая на элемент проводника

перпендикулярна плоскости треугольника, построенного на векторахи, то есть направлена перпендикулярно к проводнику, а полная сила находится суммированием. Вот, две формулы решают эту задачу.

Магнитный момент во внешнем поле

Магнитный момент сам создаёт поле, сейчас мы собственное его поле не рассматриваем, а нас интересует, как ведёт себя магнитный момент, помещённый во внешнее магнитное поле. На магнитный момент действует момент силы, равный

. Момент силы будет направлен перпендикулярно к доске, и этот момент будет стремиться развернуть магнитный момент вдоль силовой линии. Почему стрелка компаса показывает на северный полюс? Ей, конечно, нет дела до географического полюса Земли, стрелка компаса ориентируется вдоль силовой линии магнитного поля, которая, в силу случайных причин, кстати, направлена примерно по меридиану. За счёт чего? А на неё действует момент. Когда стрелка, магнитный момент, совпадающий по направлению с самой стрелкой, не совпадает с силовой линией, появляется момент, разворачивающий её вдоль этой линии. Откуда у стрелки компаса берётся магнитный момент, это мы ещё обсудим.

Кроме того, на магнитный момент действует сила, равная

. Если магнитный момент направлен вдоль, то сила втягивает магнитный момент в область с большей индукцией. Эти формулы похожи на то, как действует электрическое поле на дипольный момент, там тоже дипольный момент ориентируется вдоль поля и втягивается в область с большей напряжённостью. Теперь мы можем рассмотреть вопрос о магнитном поле в веществе.

Магнитное поле в веществе

Атомы могут обладать магнитными моментами. Магнитные моменты атомов связаны с моментом импульса электронов. Уже была получена формула

, где– момент импульса частицы создающей ток. В атоме мы имеем положительное ядро и электроне , вращающийся по орбите, на самом деле, в своё время мы увидим, что эта картина не имеет отношения к реальности, так нельзя представлять электрон, который вращается, но остаётся то, что электрон в атоме обладает моментом импульса, и этому моменту импульса будет отвечать такой магнитный момент:

. Наглядно, заряд, вращающийся по окружности, эквивалентен круговому току, то есть это элементарный виток с током. Момент импульса электрона в атоме квантуется, то есть может принимать только определённые значения, вот по такому рецепту:

,

, где вот эта величина– это постоянная Планка. Момент импульса электрона в атоме может принимать лишь определённые значения, мы сейчас не будем обсуждать, как это получается. Ну, и вследствие этого магнитный момент атома может принимать определённые значения. Эти детали нас сейчас не волнуют, но, по крайней мере, будем представлять, что атом может обладать определённым магнитным моментом, есть атомы, у которых нет магнитного момента. Тогда вещество, помещённое во внешнее поле намагничивается, а это означает, что оно приобретает определённый магнитный момент вследствие того, что магнитные моменты атомов ориентируются преимущественно вдоль поля.

Элемент объёма dV приобретает магнитный момент

, при чём векторимеет смысл плотности магнитного момента и называется вектором намагничивания. Имеется класс веществ, называемыхпарамагнетики , для которых

, намагничивается так, что магнитный момент совпадает с направлением магнитного поля. Имеютсядиамагнетики , которые намагничиваются, так сказать, «против шерсти», то есть магнитный момент антипараллелен вектору , значит,

. Это более тонкий термин. То, что векторпараллелен векторупонятно, магнитный момент атома ориентируется вдоль магнитного поля. Диамагнетизм связан с другим: если атом не обладает магнитным моментом, то во внешнем магнитном поле он приобретает магнитный момент, при чём магнитный момент антипараллелен. Этот очень тонкий эффект связан с тем, что магнитное поле влияет на плоскости орбит электронов, то есть оно влияет на поведение момента импульса. Парамагнетик втягивается в магнитное поле, диамагнетик выталкивается. Вот, чтобы это не было беспредметно, медь – это диамагнетик, и алюминий – парамагнетик, если взять магнит то алюминиевая лепёшка будет притягиваться магнитом, а тогда медная будет отталкиваться.

Понятно, что результирующее поле, когда вещество внесено в магнитное поле, это есть сумма внешнего поля и поля, создаваемого за счёт магнитного момента вещества. Теперь обратимся к уравнению

, или в дифференциальной форме

. Теперь такое утверждение: намагничивание вещества эквивалентно наведению в нём тока с плотностью

. Тогда это уравнение мы напишем в виде

.

Проверим размерность: М – это магнитный момент в единице объёма

, размерность

. Когда вы пишете какую-нибудь формулу, то размерность всегда полезно проверять, особенно если формула эта собственной выводки, то есть вы её не срисовали, не запомнили, а получили.

Намагниченность характеризуется вектором , он так и называется вектор намагниченности, это плотность магнитного момента или магнитный момент в единицу времени. Я говорил, что намагниченность эквивалентна появлению тока

, так называемого молекулярного тока, и это уравнение эквивалентно такому:

, то есть мы можем считать, что нет намагниченности, а есть такие токи. Зададимся таким уравнением:

,- это настоящие токи, связанные с конкретными носителями зарядов, аэто токи, связанные с намагниченностью. Электрон в атоме это круговой ток, возьмём область внутри, внутри образца все эти токи уничтожаются, но наличие таких круговых токов эквивалентно одному общему току, который обтекает этот проводник по поверхности, отсюда и такая формула. Перепишем это уравнение в таком виде:

,

. Этоттоже отправим влево и обозначим

, векторназываетсянапряжённостью магнитного поля , тогда уравнение приобретёт вид

. (циркуляция напряжённости магнитного поля по замкнутому контуру) = (сила тока через поверхность этого контура).

Ну, и, наконец, последнее. Мы имеем такую формулу:

. Для многих сред намагниченность зависит от напряжённости поля,

, где–магнитная восприимчивость , это коэффициент, характеризующий склонность вещества к намагничиванию. Тогда эта формула перепишется в виде

,

–магнитная проницаемость , и мы получаем такую формулу:

.

Если

, то это парамагнетики,

- это диамагнетики, ну, и, наконец, имеются вещества, для которых этопринимает большие значения (порядка 10 3),

- это ферромагнетики (железо, кобальт и никель). Ферромагнетики замечательны тем. Что они не только намагничиваются в магнитном поле, а им свойственно остаточное намагничивание, если он уже однажды был намагничен, то, если убрать внешнее поле, то он останется намагниченным в отличии от диа- и парамагнетиков. Постоянный магнит – это и есть ферромагнетик, который без внешнего поля намагничен сам по себе. Кстати, имеются аналоги этого дела в электричестве: имеются диэлектрики, которые поляризованы сами по себе без всякого внешнего поля. При наличии вещества наше фундаментальное уравнение приобретает такой вид:

,

,

.

Авот ещёпример ферромагнетика, бытовой пример магнитного поля в средах, во-первых, постоянный магнит, ну, и более тонкая вещь – магнитофонная лента. Каков принцип записи на ленту? Магнитофонная лента - это тонкая лента, покрытая слоем ферромагнетика, записывающая головка - это катушка с сердечником, по которой течёт переменный ток, в зазоре создаётся переменное магнитное поле, ток отслеживает звуковой сигнал, колебания с определённой частотой. Соответственно, в контуре магнита имеется переменное магнитное поле, которое меняется вместе с этим самым током. Ферромагнетик намагничивается переменным током. Когда эта лента протягивается по устройству такого типа, переменное магнитное поле создаёт переменную э.д.с. и воспроизводится опять электрический сигнал. Это ферромагнетики на бытовом уровне.

Закон Био - Савара - Лапласа для проводника с током I , элемент которого dl создает в некоторой точке А (рис. 164) индукцию поля dB , записывается в виде

где dl - вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r - радиус-вектор,

проведенный из элемента dl проводника в точку А поля, r - модуль радиуса-векто­ра г. Направление dB перпендикулярно dl и r , т. е. перпендикулярно плоскости, в ко­торой они лежат, и совпадает с каса­тельной к линии магнитной индукции. Это направление может быть найдено по пра­вилу нахождения линий магнитной индук­ции (правилу правого винта): направле­ние вращения головки винта дает направ­ление dB , если поступательное движение винта соответствует направлению тока в элементе.

Модуль вектора dB определяется вы­ражением

где а - угол между векторами dl и г.

Для магнитного поля, как и для элек­трического, справедлив принцип суперпо­зиции: магнитная индукция результирую­щего поля, создаваемого несколькими то­ками или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каж­дым током или движущимся зарядом в от­дельности:

Расчет характеристик магнитного поля (В и Н ) по приведенным формулам в об­щем случае довольно сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био - Савара - Лапласа совместно с принци­пом суперпозиции позволяет довольно просто рассчитать конкретные поля. Рас­смотрим два примера.

1. Магнитное поле прямого тока - тока, текущего по тонкому прямому про воду бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одина­ковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве по­стоянной интегрирования выберем угол а (угол между векторами dl и r ), выразив через него все остальные величины. Из рис. 165 следует, что

(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что маг­нитная индукция, создаваемая одним эле­ментом проводника, равна

Так как угол а для всех элементов прямо­го тока изменяется в пределах от 0 до я, то, согласно (110.3) и (110.4),

Следовательно, магнитная индукция поля прямого тока

2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следу­ет из рисунка, все элементы кругового проводника с током создают в центре магнитное поле одинакового направления - вдоль нормали от витка.

Поэтому сложе­ние векторов dB можно заменить сложени­ем их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina=1) и расстояние всех эле­ментов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),

Следовательно, магнитная индукция поля в центре кругового проводника с током

18. Поток магнитного поля. Теорема Гаусса для Ḃ.

Потоком вектора магнитной индукции (магнитным потоком) через площадку наз. скалярная величина , где угол между векторами (вектор нормали к плоскости контура) и .

Единица : вебер (Вб)..

Для однородного поля и плоской поверхности, расположенной перпендикулярно вектору : . Магнитный поток сквозь поверхность с площадью находится алгебраическим суммированием потоков сквозь участки поверхности.

Теорема Гаусса: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю: .

Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

19. Теорема о циркуляции вектора Ḃ, её применение к расчету полей. Поле соленоида.

Теорема о циркуляции вектора В имеет в учении о магнитном поле такое же значение как теорема Гаусса в электростатике, так как позволяет находить магнитную индукцию поля без применения закона Био-Савара-Лапласа.

1). Продемонстрируем справедливость теоремы о циркуляции вектора В на примере магнитного поля прямого тока 1 , перпендикулярного плоскости чертежа и направленного к нам (рис. 13). Представим себе замкнутый контур в виде окружности радиуса r . В каждой точке этого контура вектор В одинаков по модулю и направлен по касательной к окружности. Следовательно, циркуляция вектора В равна

Рис.13 . Рис.14 .

Согласно выражению (9.2), получим В 2πr = μ o I (в вакууме), откуда В = μ o I /(2πr ).

Таким образом, исходя из теоремы о циркуляции вектора В , получили выражение для магнитной индукции поля прямого тока, выведенное выше (2.6).

2). Рассчитаем индукцию магнитного поля внутри соленоида – цилиндрической катушки, состоящей из большого числа витков равномерно намотанных на общий сердечник . Рассмотрим соленоид длиной l , имеющий n витков, по которому течет ток I (рис.14). Длину соленоида считаем во много раз большей, чем диаметр его витков, т.е. рассматриваемый соленоид бесконечно длинный. Экспериментальное изучение магнитного поля соленоида, проведенное с помощью железных опилок показывает, что внутри соленоида поле является однородным, вне соленоида неоднородным и очень слабым, т.е. его можно практически считать равным нулю.

Циркуляция вектора В по замкнутому контуру, совпадающему с одной из линий магнитной индукции, АВСDА , и охватывающему все n витков согласно (9.2), равна

. (10.1)

Интеграл по АВСDА можно представить в виде двух – по внешнему участку ABCD (он равен нулю, так как вне соленоида В =0) и по внутреннему DA .

.

На участке DА циркуляция вектора В равна Вl (контур совпадает с линией магнитной индукции); следовательно,

.

Отсюда приходим к выражению для магнитной индукции поля внутри соленоида (в вакууме):

B =μ o nI / l . (10.2)

Получили, что поле внутри соленоида однородно.

3). Важное значение для практики имеет также магнитное поле тороида – кольцевой катушки, витки которой намотаны на сердечник, имеющий форму тора . Магнитное поле сосредоточено внутри тороида, вне его поле отсутствует. Тороид можно рассматривать как достаточно длинный соленоид свитый в кольцо и для расчета напряженности магнитного поля тороида пользоваться формулой (10.2):

В = μ o nI /l = μ o nI /(2πr ). (10.3)

Сила Ампера.

Сила Ампера это та сила, с которой магнитное поле действует на проводник, с током помещённый в это поле. Величину этой силы можно определить с помощью закона Ампера. В этом законе определяется бесконечно малая сила для бесконечно малого участка проводника. Что дает возможность применять этот закон для проводников различной формы.

Формула 1 - Закон Ампера

B индукция магнитного поля, в котором находится проводник с током

I сила тока в проводнике

dl бесконечно малый элемент длинны проводника с током

альфа угол между индукцией внешнего магнитного поля и направлением тока в проводнике

Направление силы Ампера находится по правилу левой руки. Формулировка этого правила, звучит так. Когда левая рука расположена таким образом, что лини магнитной индукции внешнего поля входят в ладонь, а четыре вытянутых пальца указывают направление движения тока в проводнике, при этом отогнутый под прямым углом большой палец будет указывать направление силы, которая действует на элемент проводника.

Рисунок 1 - правило левой руки

Некоторые проблемы возникают, при использовании правила левой руки, в случае если угол между индукцией поля и током маленький. Трудно определить, где должна находиться открытая ладонь. Поэтому для простоты применения этого правила, можно ладонь располагать так, чтобы в нее входил не сам вектор магнитной индукции, а его модуль.

Из закона Ампера следует, что сила Ампера будет равна нулю, если угол между линией магнитной индукции поля и током будет равен нулю. То есть проводник будет располагаться вдоль такой линии. И сила Ампера будет иметь максимально возможное значение для этой системы, если угол будут составлять 90 градусов. То есть ток будет перпендикулярен линии магнитной индукции.

С помощью закона Ампера можно найти силу, действующую в системе из двух проводников. Представим себе два бесконечно длинных проводника, которые находятся на расстоянии друг от друга. По этим проводникам протекают токи. Силу, действующую со стороны поля создаваемого проводником с током номер один на проводник номер два можно представить в виде.

Значение магнитной индукции для любого проводника определяется законом Био - Савара - Лапласа.

-в векторной форме, (15.6)

- в скалярной форме. (15.7)

Вектор всегда перпендикулярен плоскости, построенной на векторах и . С помощью закона Био - Савара - Лапласа рассчитаем магнитную индукцию поля прямого, кругового и соленоидального токов.

Вывод формулы напряжённости магнитного поля прямого тока (рис. 15.9; рис. 15.10) .

Применим формулу

для вычисления полей простейших токов. Рассмотрим поле, создаваемое током, текущим по бесконечному прямому проводу (Рис. 15.9) .Все dBв данной точке имеют одинаковое направление. Поэтому сложение векторов dBможно заменить сложением их модулей. Точка, для которой мы вычисляем магнитную индукцию, находится на расстоянии b от провода. Из рисунка 15.9 видно, что:

Подставим эти значения в формулу магнитной индукции:

.

Угол для всех элементов бесконечно прямого тока изменяется в пределах от 0 до . Следовательно:

.

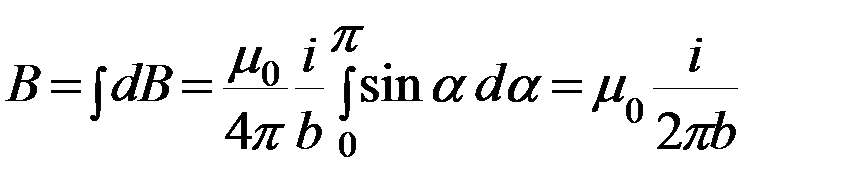Таким образом, магнитная индукция поля прямого тока определяется формулой: . (15.8)

Для того, чтобы получить напряженность магнитного поля, необходимо разделить правую часть формулы (15.8) на :

. (15.9)

Вывод формулы напряжённости магнитного поля кругового тока (рис. 15.11).

Рассмотрим поле, создаваемое током, текущим по тонкому проводу, имеющему форму окружности (круговой ток). Определим магнитную индукцию кругового тока

Рассмотрим индукции , создаваемых двумя элементами контура dl 1 и dl 2 . Т. к. угол между r и dl равен 90°, то sin 90°=1.

Закон Био - Савара - Лапласа для двух элементов:

Выбрав dl 1 =dl 2 и принимая, что r 1 =r 2 , получим:

Проинтегрируем это выражение по всему контуру и заменим r на получим:

(15.10)

В частности, при x=0 имеем:

(15.11)

магнитная индукция в центре кругового тока

Напряженность магнитного поля в центре кругового тока равна:

(15.12)

Формула для расчета напряженности магнитного поля кругового тока на его оси принимает вид:

(15.13)

Вывод формулы напряжённости магнитного поля соленоидального тока.

Соленоид представляет собой тонкий провод, навитый плотно, виток к витку, на цилиндрический каркас. В отношении создаваемого им поля соленоид эквивалентен системе одинаковых круговых токов с общей прямой осью. Бесконечно длинный соленоид симметричен относительно любой перпендикулярной к его оси плоскости. Взятые попарно симметричные относительно такой плоскости витки создают поле, магнитная индукция которого перпендикулярна к плоскости. Следовательно, в любой точке внутри и вне соленоида вектор может иметь лишь направление, параллельное оси.

Возьмем прямоугольный контур 1-2-3-4. Циркуляцию вектора по этому контуру можно представить следующим образом:

Из четырех интегралов, стоящих в правой части, второй и четвертый равны нулю, так как вектор перпендикулярен к участкам контура, по которым они берутся.

Взяв участок 3-4 на большом расстоянии от соленоида(где поле заведомо должно быть очень слабым), третьим слагаемым можно пренебречь. Следовательно, можно утверждать, что:

Здесь В - магнитная индукция поля в тех точках, где располагается отрезок 1-2, -длина этого отрезка.

Если отрезок 1-2 проходит внутри соленоида на любом расстоянии от его оси, контур охватывает суммарный ток , где - число витков соленоида, приходящееся на единицу его длинны, - сила тока в соленоиде. Поэтому согласно:

Откуда: (15.14)

а напряженность магнитного поля соленоидального тока равна:

(15.15)

Отметим, что полученный нами результат не зависит от того, на каком расстоянии от оси (но внутри соленоида) располагается отрезок 1-2. Если этот отрезок располагается вне соленоида, то охватываемый контуром ток равен нулю, вследствие чего:

.

Откуда В=0. Таким образом, вне бесконечного длинного соленоида магнитная индукция равна нулю, внутри - всюду одинакова и имеет величину, определяемую формулой (15.14). По этой причине в учении о магнетизме бесконечно длинный соленоид играет такую же роль, как плоский конденсатор в учении об электричестве. В обоих случаях поле однородно и полностью заключено внутри конденсатора (электрическое) и внутри соленоида(магнитное).

Произведение называется числом ампер - витков на метр.

Тесты к лекции №15

Тест 15.1.Магнитная индукция поля, создаваемого отрезком бесконечно тонкого прямолинейного проводника, вычисляется по формуле…

£

£

£

£

Тест 15.2.Магнитная индукция в центре кругового тока определяется по формуле…

£

£

£

£

Тест 15.3.Форма существования материи, обладающая свойством передавать магнитное взаимодействие.

£ магнитное поле

£ магнитная индукция

£ пробный контур

£ магнитный момент

Тест 15.4.Дайте определение пробного контура.

£ контур, вносящий помехи в исходное поле.

£ контур, усиливающий исходное поле.

£ контур, ослабляющий исходное поле.

£ контур, который не создает заметных искажений исходного поля.

Тест 15.5.Формула выражает:

£ вектор магнитной индукции

£ напряженность магнитного поля

£ магнитную индукцию

£ магнитный момент

Вихревой характер магнитного поля. Циркуляция вектора индукции магнитного поля. Магнитный поток. Сила Ампера. Работа по перемещению проводника с током в магнитном поле. Сила Лоренца. Определение удельного заряда электрона

16.1. Вихревой характер магнитного поля. Циркуляция вектора индукции магнитного поля. Магнитный поток

16.2. Сила Ампера

16.3. Работа по перемещению проводника с током в магнитном поле

16.4. Сила Лоренца

16.5. Определение удельного заряда электрона